Writing Linear Equations From A Table

Part I. How Linear Equations relate to Tables Of Values

Equations as Relationships

The equation of a line expresses a relationship between x and y values on the coordinate plane. For instance, the equation $$y = x$$ expresses a relationship where every x value has the exact same y value. The equation $$ y = 2x $$ expresses a relationship in which every y value is double the x value, and $$ y = x + 1 $$ expresses a relationship in which every y value is 1 greater than the x value.

So what about a Table Of Values?

Since, as we just wrote, every linear equation is a relationship of x and y values, we can create a table of values for any line. These are just the $$ x $$ and $$ y $$ values that are true for the given line. In other words, a table of values is simply some of the points that are on the line.

Example 1

Equation: $$ \red y = \blue x + 1 $$

Table of Values

$$ \blue x \text { value} $$	Equation	$$ \red y \text{ value} $$
	y = x + 1
$$ \blue 3 $$	$$y = ( \blue 3 ) + 1$$	$$ \red 4 $$
$$ \blue 4 $$	y = ($$ \blue 4 $$ ) + 1	$$ \red 5 $$
$$ \blue 5 $$	$$ y = (\blue 5 ) + 1$$	$$ \red 6 $$
$$ \blue 6 $$	$$ y = ( \blue 6) + 1 $$	$$ \red 7 $$

Example 2

Equation: y = 3x + 2

Table of Values

X Value	Equation	Y value
	y = 3x + 2
1	y = 3(1) + 2	5
2	y = 3(2) + 2	7
3	y = 3(3) + 2	11
4	y = 3(4) + 2	14

So, to create a table of values for a line, just pick a set of x values, substitute them into the equation and evaluate to get the y values.

Practice Creating a Table of Values

Problem 1

Original problem
Step 1
Step 2
Step 3
Step 4

Create a table of values of the equation y = 5x + 2.

Create the table and choose a set of x values.

X Value	Equation	Y value
	y = 5x + 2
1
2
3
4

Substitute each x value (left side column) into the equation.

X Value	Equation	Y value
	y = 5x + 2
1	y = 5(1) + 2
2	y = 5(2) + 2
3	y = 5(3) + 2
4	y = 5(4) + 2

Evaluate the equation (middle column) to arrive at the y value.

X Value	Equation	Y value
	y = 5x + 2
1	y = 5(1) + 2	7
2	y = 5(2) + 2	12
3	y = 5(3) + 2	17
4	y = 5(4) + 2	22

An Optional step, if you want, you can omit the middle column from your table, since the table of values is really just the x and y pairs.
(We used the middle column simply to help us get the y values)

X Value	Y Value

1	7
2	12
3	17
4	22

Problem 2

Original problem
Step 1
Step 2
Step 3
Step 4

Create a table of values of the equation y = −6x + 2.

Create the table and choose a set of x values.

X Value	Equation	Y value
	y = −6x + 2
1
2
3
4

Substitute each x value (left side column) into the equation.

X Value	Equation	Y value
	y = −6x + 2
1	y = −6(1) + 2
2	y = −6(2) + 2
3	y = −6(3) + 2
4	y = −6(4) + 2

Evaluate the equation (middle column) to arrive at the y value.

X Value	Equation	Y value
	y = −6x + 2
1	y = −6(1) + 2	-4
2	y = −6(2) + 2	-10
3	y = −6(3) + 2	-16
4	y = −6(4) + 2	-22

An Optional step, if you want, you can omit the middle column from your table, since the table of values is really just the x and y pairs .(We used the middle column simply to help us get the y values)

X Value	Y value

1	-4
2	-10
3	-16
4	-22

Problem 3

Original problem
Step 1
Step 2
Step 3
Step 4

Create a table of values of the equation y = −6x − 4

Create the table and choose a set of x values

X Value	Equation	Y value
	y = −6x − 4
1
2
3
4

Substitute each x value (left side column) into the equation.

X Value	Equation	Y value

1	y = −6(1) − 4
2	y = −6(2) − 4
3	y = −6(3) − 4
4	y = −6(4) − 4

Evaluate the equation (middle column) to arrive at the y value.

X Value	Equation	Y value

1	y = −6(1) − 4	-10
2	y = −6(2) − 4	-16
3	y = −6(3) − 4	-22
4	y = −6(4) − 4	-28

An Optional step, if you want, you can omit the middle column from your table, since the table of values is really just the x and y pairs. (We used the middle column simply to help us get the y values)

X Value	Y value

1	-10
2	-16
3	-22
4	-28

Part II. Writing Equation from Table of Values

Often, students are asked to write the equation of a line from a table of values. To solve this kind of problem, simply chose any 2 points on the table and follow the normal steps for writing the equation of a line from 2 points.

Problem 4

Original problem
Step 1
Step 2
Step 3
Step 4

Choose any two x, y pairs from the table and calculate the slope. Since, I like to work with easy, small numbers I chose (0, 3) and (1, 7).

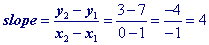
Slope from Table

X Value	Y value
0	3
1	7
2	11
3	15

Find the value of 'b' in the slope intercept equation.

y = mx + b
y = 4x + b

Since our table gave us the point (0, 3) we know that 'b' is 3. Remember 'b' is the y-intercept which, luckily, was supplied to us in the table.

Answer: y = 4x + 3

If you'd like, you could check your answer by substituting the values from the table into your equation. Each and every x, y pair from the table should work with your answer.

Problem 5

Original problem
Step 1
Step 2
Step 3
Step 4

Write the equation from the table of values provided below.

X Value	Y value
2	8
4	9
6	10

Find the value of 'b' in the slope intercept equation.

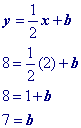
eqauation

Now that we know the value of b, we can substitute it into our equation.

Answer: y = ½x + 7

If you'd like, you could check your answer by substituting the values from the table into your equation. Each and every x, y pair from the table should work with your answer.

Problem 6

Original problem
Step 1
Step 2
Step 3
Step 4

Find the value of 'b' in the slope intercept equation.

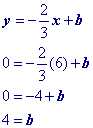
eqauation

Now that we know the value of b, we can substitute it into our equation.

Answer: y = 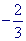two thirds x + 4

If you'd like, you could check your answer by substituting the values from the table into your equation. Each and every x, y pair from the table should work with your answer.

Challenge Problem

Why can you not write the equation of a line from the table of values below?

X Value	Y value
0	1
1	3
2	8
3	11

The reason that this table could not represent the equation of a line is because the slope is inconsistent. For instance the slope of the 2 points at the top of the table (0, 1) and (1, 3) is different from the slope at the bottom (2, 8) and (3, 11).

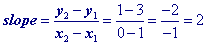
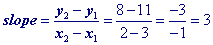
slope1 slope2